x <- TDA::torusUnif(n = 200, a = 1, c = 2)
pd <- TDA::alphaComplexDiag(x, maxdimension = 2)
plot(pd$diagram, asp = 1)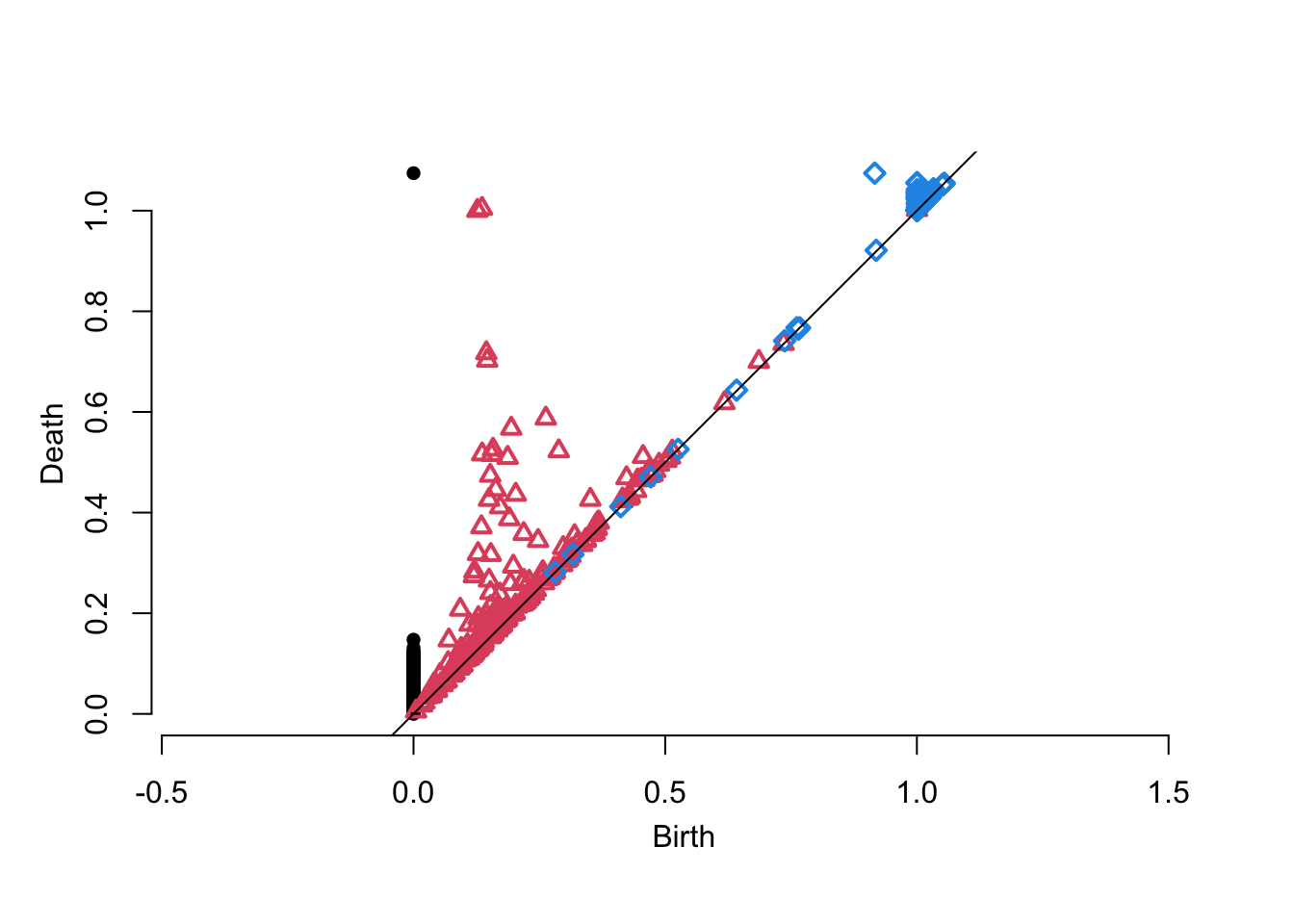
Jason Cory Brunson, Alexsei Luchinsky, Umar Islambekov
June 4, 2025
Topological data analysis (TDA) is a pretty mature discipline at this point, but in the last several years its assimilation into machine learning (ML) has really taken off. Based on our experience, the plurality of experimental TDA tools are written in Python, and naturally Python is home to most of these applications.
That’s not to say that there are no R packages for TDA-ML. {TDAkit}, {TDApplied}, and others provide tools for specific self-contained analyses and could be used together in larger projects. As with the broader R ecosystem, though, their integration can require some additional work. The combination of several low-level libraries and compounding package dependencies has also made this toolkit fragile, with several packages temporarily or permanently archived.
Meanwhile, the Tidymodels package collection has enabled a new generation of users, myself (JCB) included, to build familiarity and proficiency with conventional ML. By harmonizing syntax and smoothing pipelines, Tidymodels makes it quick and easy to adapt usable code to new data types, pre-processing steps, and model families. By using wrappers and extractors, it also allows seasoned users to extend their work beyond its sphere of convenience.
We therefore think that Tidymodels is an ideal starting point for a more sustained and interoperable collection for TDA-ML in R. Since much of the role of TDA in ML has been to extract and vectorize features from spatial, image, and other high-dimensional data, we present an extension to {recipes} for just this purpose. Assembling a comprehensive, general-purpose toolkit is a long-term project. Our contribution is meant to spur that project on.
We present two packages: {TDAvec}, an interface to several efficient feature vectorizations, and {tdarec}, a {recipes} + {dials} extension that integrates these vectorizations into Tidymodels. First, though, we need to introduce persistent homology and how it can be computed with R.
In predictive modeling, persistent homology (PH) is the workhorse of TDA.1 In a nutshell, it measures topological patterns in data—most commonly clusters and enclosures—by the range of resolutions through which they persist. Several packages interface to lower-level libraries that compute PH for various data structures—all accept point clouds and distance matrices, but other structures are accepted where noted:
Here is an example using the most mature package, {TDA}, to compute the PH for an alpha filtration of a sample from a torus:
x <- TDA::torusUnif(n = 200, a = 1, c = 2)
pd <- TDA::alphaComplexDiag(x, maxdimension = 2)
plot(pd$diagram, asp = 1)
We rely for now on {ripserr} to compute PH, but a near-term upgrade will incorporate {TDA} as well.
Vectorization is a crucial step to bridge TDA and ML. Numerous methods have been proposed, and research shows that ML performance on a specific task can depend strongly on the chosen method. Therefore, it is highly desirable to compare several approaches to a given problem and select the one found to be best-suited to it.
Although most proposed vectorization methods are available in free software, they are scattered across various R and Python packages. This complicates the comparison process, as researchers must search for available methods and adapt their code to the interface of each specific implementation. The goal of {TDAvec} (Luchinsky and Islambekov 2025) is to address this issue.
We (AL and UI) have consolidated all currently available vectorizations (of which we are aware) and implemented them in a single R library. Some of these vectorizations are parameter-free, but others rely on one or several hyperparameters. For ease of comparison, we also use a consistent interface, with a common camelcase naming convention, e.g. computePersistenceLandscape(). Additionally, several new vectorization methods developed by our group are also available within the TDAvec framework.
Here, for example, is how to compute the tropical coordinates proposed by Kališnik (2019) and a coarse vectorization of our own persistence block transformation (Chan et al. 2022) for the degree-1 layer of the persistence diagram above:
F1 F2 F3 F4 F5 F6
0.8733197 1.7413925 2.3140151 2.8699513 10.6196686 6.4755658
F7
216.8694742 xy_seq <- seq(0, 1.5, .5)
computePersistenceBlock(
pd$diagram, homDim = 2,
xSeq = xy_seq, ySeq = xy_seq
)[1] 0.4635279 0.2768490 0.0000000 0.2799298 60.0256117 66.5632299 0.0000000
[8] 70.2769208 84.9905249Notably, all vectorizations are written in C++ and exposed to R using {Rcpp}. We also utilize the Armadillo package for various matrix operations, which makes all computations extremely fast and efficient.
{recipes} is the pre-processing arm of Tidymodels; mostly it provides step_*() functions that pipe together as recipe specifications, to later be applied directly to data or built into workflows. {dials} provides tuning functions for these steps as well as for model families provided by {parsnip}.
{tdarec} provides two primary families of steps:
step_pd_*() for persistence diagram. These steps rely on the engines above and are scoped according to the underlying mathematical object encoded in the data: Currently the {ripserr} engine handles point clouds (encoded as coordinate matrices or distance matrices) and rasters (encoded as numerical arrays). These steps accept list-columns of data sets and return list-columns of persistence diagrams.step_vpd_*() for vectorized persistence diagram. These steps rely on {TDAvec} and are scoped as there by transformation. They accept list-columns of persistence diagrams and return numeric columns (sometimes flattened from matrix output, e.g. multi-level persistence landscapes) that can be used by most predictive model families.Here is how to incorporate PH (using the default Vietoris–Rips filtration) and the persistence block transformation above into a pre-processing recipe:
suppressMessages(library(tdarec))
dat <- tibble(source = "torus", sample = list(x))
recipe(~ sample, data = dat) |>
step_pd_point_cloud(sample, max_hom_degree = 2) |>
step_pd_degree(sample_pd, hom_degrees = 2) |>
step_vpd_persistence_block(
sample_pd_2,
hom_degree = 2, xseq = xy_seq
) -> rec1 package (ripserr) is needed for this step but is not installed.To install run: `install.packages("ripserr")`The code chunk uses the additional step step_pd_degree() to extract degree-specific layers from multi-degree persistence diagrams; in this case, we are interested in vectorizing only 2-dimensional features. Despite this, we must also specify the degree of the features we want in the persistence block step.
Many methods remain to be built into these tools, which will only reach their full potential through user feedback. Two issues in particular, additional vectorizations for {TDAvec} and additional engines for {tdarec}, may remain open—or, ahem, persist—into the foreseeable future. We welcome bug reports, feature requests, and code contributions from the community!
Exploratory modeling is another story.↩︎